Discover more from Cryptoeconomic Systems Journal & Conference Series
MIT DCI's Cryptocurrency Research Review #3
Bulletproofs, central bank digital currency, and Spice
Hello!
Welcome to Cryptocurrency Research Review, Issue No. 3! This publication (curated by the MIT Media Lab’s Digital Currency Initiative in partnership with MIT Press) crowdsources high-quality reviews of interdisciplinary research from the fields of cryptocurrency and blockchain technology. We intend this publication to help surface impactful work in the space, provide more neutral analysis of ongoing research, and to encourage interdisciplinary discussions in the community.
This is an experimental effort to figure out how best to meet the needs of cryptocurrency and blockchain technology researchers. If you have any feedback, please respond to this email directly!
We hope you enjoy this issue. Let’s get right to it!
Building, and building on, Bulletproofs
By Cathie Yun, Interstellar
Preface
In this post, I will explain how the Bulletproofs zero knowledge proof protocol works, as well as talk about the confidential asset protocol and confidential smart contract language we are building using Bulletproofs.
This post is a condensed version of previous talks and blog posts and our Bulletproofs library documentation.
Background
Zero-knowledge range proofs are a key building block for confidential payment systems, such as Confidential Transactions for Bitcoin, Monero, and Mimblewimble, Confidential Assets, and many other protocols. Range proofs allow a verifier to ensure that secret values, such as asset amounts, are nonnegative. This prevents a user from forging value by secretly using a negative amount. Since every transaction involves one or more range proofs, their efficiency, both in terms of proof size and verification time, is key to transaction performance.
In 2017, Bünz, Bootle, Boneh, Poelstra, Wuille, and Maxwell published Bulletproofs, which dramatically improves proof performance both in terms of proof size and verification time. In addition, it allows for proving a much wider class of statements than just range proofs.
Definitions
Commitment - a commitment Com(m)to message m is hiding, which means it does not reveal m. It is also binding, which means that if you make a commitment to m, you cannot open it to a different message m’. In the context of Bulletproofs, commitment refers to a Pedersen commitment, which has the additional property of being additively homomorphic, which means that Com(a) + Com(b) = Com(c) only if a + b = c.
Zero-knowledge proof - a proof that a certain statement is true, without revealing the secret that the statement is about. This is usually done by making a commitment to the secret that the statement is about, and sharing the commitment along with the proof.
Zero-knowledge range proof - a proof that a secret value is in a certain range (from 0 to 2^n - 1). The proof is usually shared with a commitment to the secret value so that it can be verified.
Inner product - the sum of an entry-wise multiplication of two vectors.
Notation: vectors are written in bold, such as a, 2^n (which is an n length vector 2^0, 2^1, … 2^{n-1}), and 0^n (which is an n length vector of 0s). Inner products are written as c = <a, b>, where a and b are vectors of the same length, and c is a scalar.
Building a Bulletproof range proof
We’d like to make a proof of the following statement:

We know that if this is true, then v must be a binary number of length n. For example, if n=4 and v=3 (we’re checking if 3 is in range of 0 to 2^4 - 1), then this means that v must be able to be broken up into a bit representation that is 4 bits long, if it is actually in range:
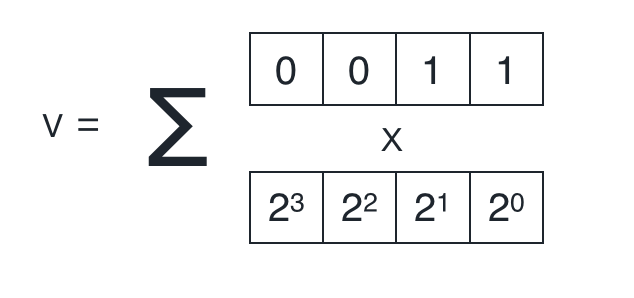
We would like to represent this claim in the form of an inner product because of the extremely efficient inner product proof that Bulletproof introduces, which we will talk about in the next section.
First, let’s name the bit representation of v v_bits.
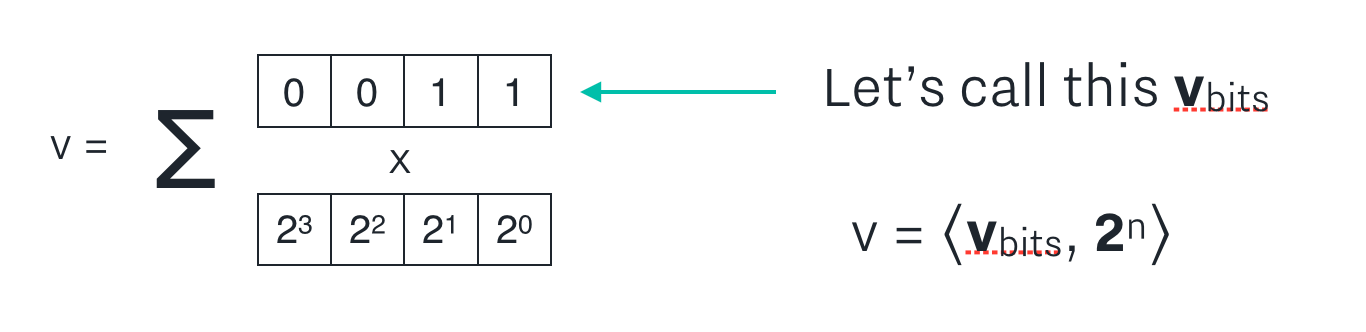
v should be equal to the inner product of v_bits and the vector 2^n (which is an n length vector 2^0, 2^1, … 2^{n-1}) if v_bits is actually the bit representation of v. We can do that by adding check 1 in the figure below.
Also, we need to make sure that v_bits is actually composed only of bits (no other pesky numbers, like 5 or -1000... that would be bad!) We can do that by adding check 2 in the figure below.
Next, we combine these two statements using challenge scalars, and add blinding factors to them. The math behind this is not difficult - just tedious - and ends up giving us an inner product statement in the form of c = <a, b>. That is, we arrive at a statement where if the statement is true, then we know that v is in range of 0 and 2^n. You can follow along with the step-by-step math for how that statement is created in our range proof notes.
Inner Product Proof
In the range proof section, I mentioned that our goal was to create a statement in the form of an inner product, for efficiency reasons. Let’s go into more detail on what an inner product is, and how we can prove an inner product efficiently!
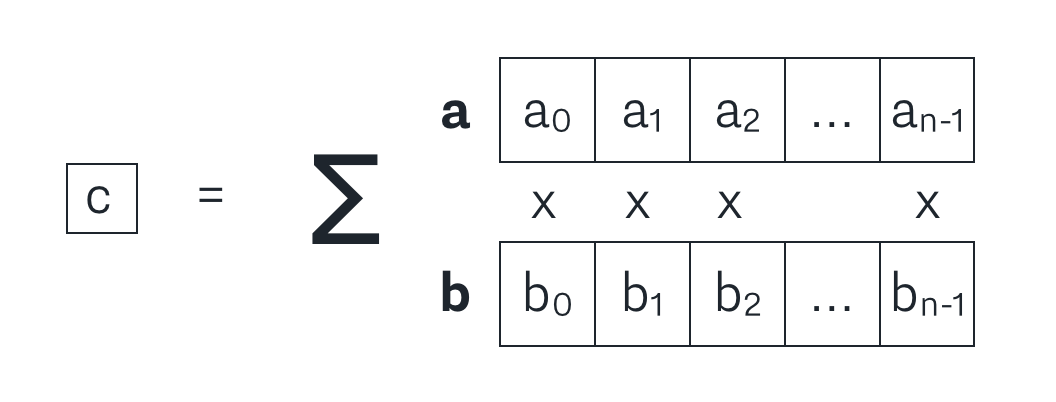
An inner product proof is a proof that c is the inner product of vectors a and b. That is,
c = <a, b>
This may be a helpful visual for what an inner product is:
Naively, a prover could prove this to the verifier by sending over a and b and c, and then the verifier could verify that c = <a, b> by computing it themself. However, this would take O(n) space to send, and O(n) time to verify, where n is the length of a and b. The great thing about the bulletproofs inner product proof is that it allows us to do this proof in O(log(n)) time and space instead!
The intuition for how the inner product proof achieves this efficiency, is that in each step it halves the size of the a and b vectors it is working with. Therefore, it requires log(n) steps since after that many steps, the lengths of a and b are 1 (the base case).
So if we started with the original a and b vectors, and their product c, then we can divide each of the vectors into a hi and lo half:

And then, we get a random challenge scalar x that we use to combine the hi and low halves of a and b to create a’ and b’, which also gives us a new c’ = <a', b'>.
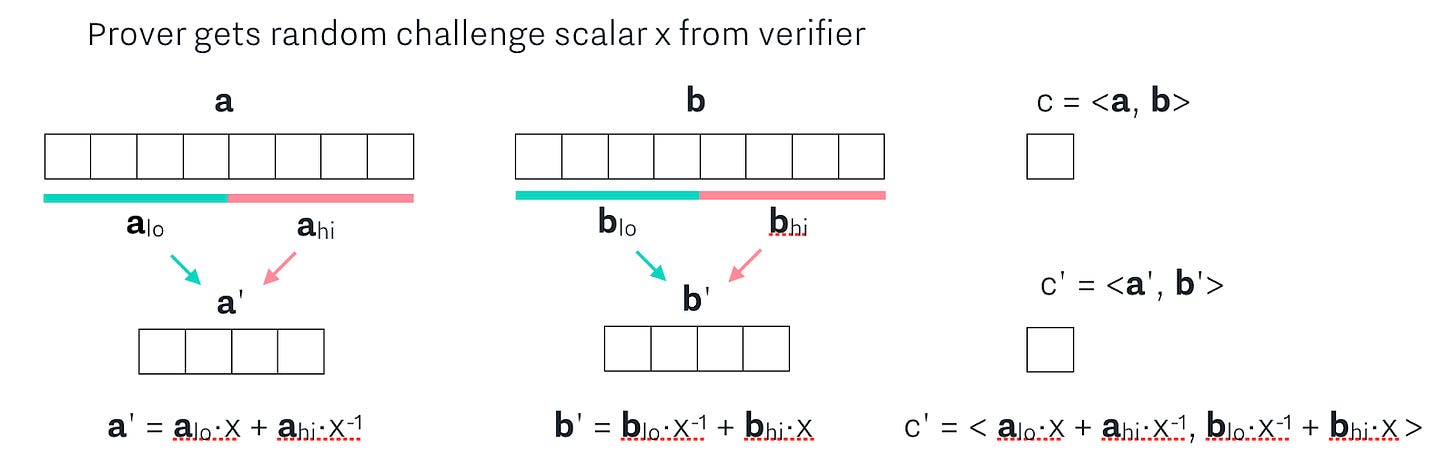
When doing the math to expand c’, notice that the first two terms of c’ are the same as c! Therefore, we can simplify the expression for c’ to be written in relation to c, and what we can call terms L and R:
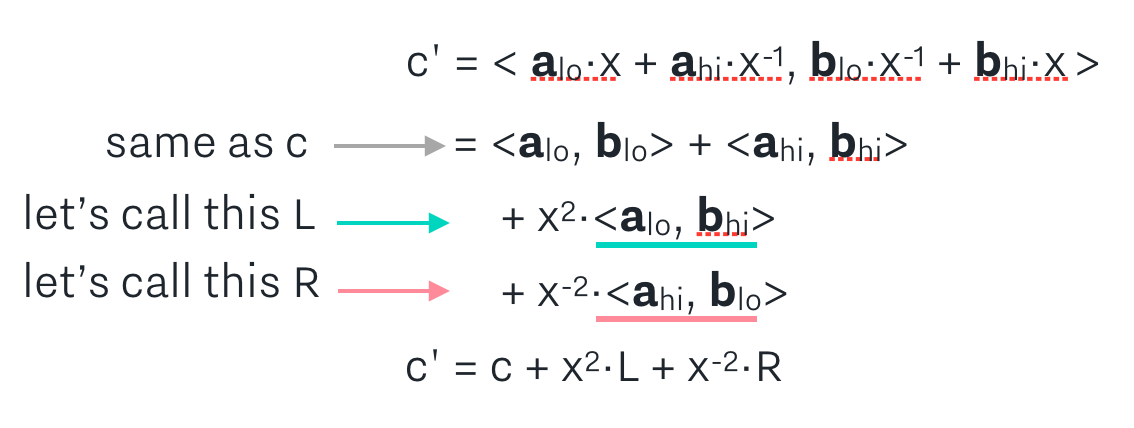
In each round, the prover sends L and R to the verifier, and repeats the next round using the a’, b’, c’ as a, b, c. Notice how at each step, this halves the lengths of the vectors a and b!
After log(n) steps, we arrive at the base case, where a’ and b’ are both of length 1. Then, there is no more compression to be done, and the prover can simply send a’, b’, c’ to the verifier.
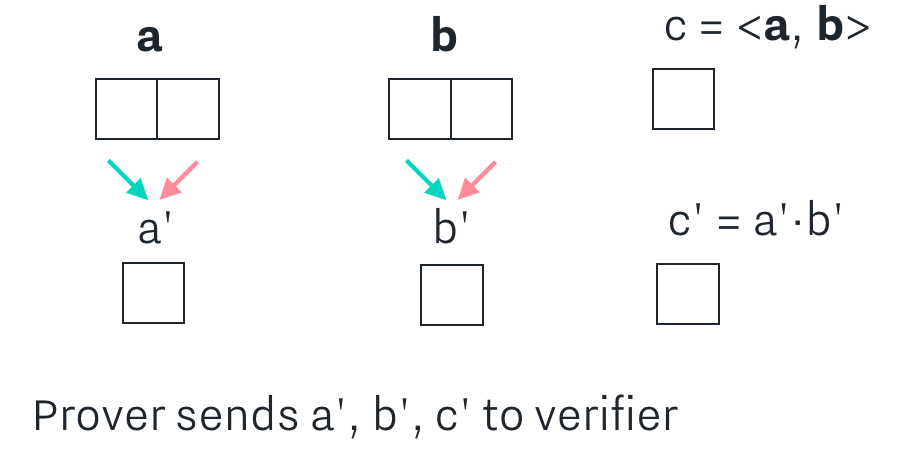
The verifier now has scalars a’, b’, c’ from the base case, and scalars L and R from each of the log(n) steps. The verifier can then reverse the process, starting at the base case. They can trivially verify the base case by checking that c’ = a’ * b’. They can check that the computation is done correctly at each higher step by verifying the calculation of c by using the c’, L, R from that step, until they have completed all checks.
To see the full math behind the inner product proof, read our inner product proof notes. To see the prover and verifier’s algorithms, read our inner product proof protocol notes.
Aggregated Range Proof
Aggregated range proofs are great for performance, because they allow m parties to produce an aggregated proof of their individual statements (m range proofs), such that the aggregated proof is smaller and faster to verify than m individual range proofs. The protocol for creating aggregated proofs is slightly more complex than creating individual range proofs, and requires a multi-party computation involving the parties. In our implementation, we used a centralized dealer to coordinate the communication between the m participating parties.
To see the math behind the aggregated proof, see our aggregated range proof notes. To see the prover and verifier’s algorithms, read our range proof protocol notes. Also of potential interest is our notes on the aggregation multi-party computation protocol and corresponding blog post.
Constraint System Proof
A constraint system is a collection of two kinds of constraints:

Constraint systems are very powerful because they can represent any efficiently verifiable program. A zero knowledge constraint system proof is a proof that all of the constraints in a constraint system are satisfied by certain secret inputs, without revealing what those secret inputs are.
For example, we can make a set of constraints (a “gadget”) that enforces that some outputs are a valid permutation of some inputs. Let’s call this a shuffle gadgets. In a simple shuffle gadget with only two inputs and two outputs, we could represent the possible states as the following:
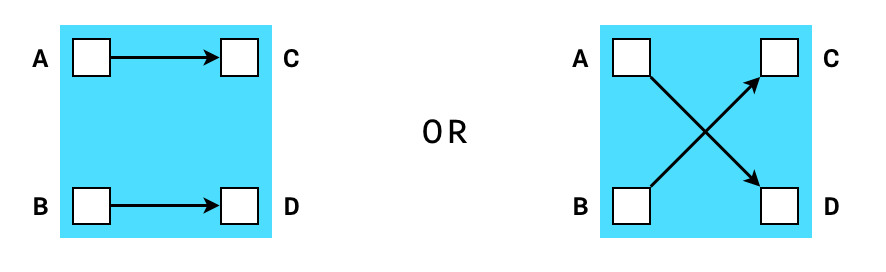
If we get a random scalar x, then we can actually express this requirement in the form of an equation: (A - x) * (B - x) = (C - x) * (D - x). Because of the equality of polynomials when roots are permuted, we know that if the equation holds for a random x, then {A, B} must equal {C, D} in any order.
When we implement this 2-shuffle gadget in our constraint system, it looks like this:
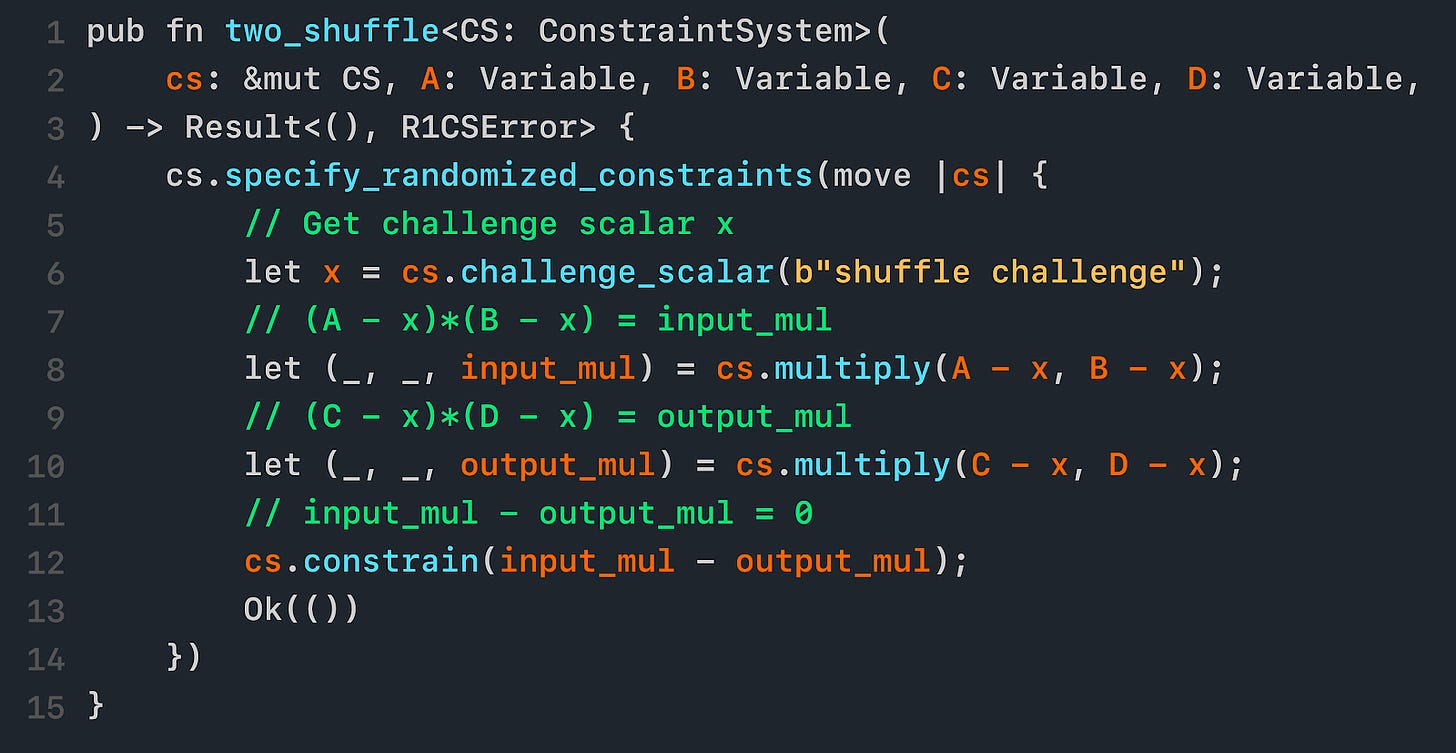
In line 6, we get our challenge scalar x.
In line 8 and 10, we make two multiplication constraints: (A - x) * (B - x) = input_mul and (C - x) * (D - x) = output_mul.
In line 12, we make one linear constraint: input_mul - output_mul = 0, which constrains input_mul = output_mul.
For the full sample code of the 2-shuffle gadget, including tests, see our GitHub repo.
For an overview of how and why we implemented constraint system proofs, read our blog post here.
To see the math behind constraint system proofs, read our r1cs proof notes.
Cloak
The goal of a Confidential Assets scheme is to make transactions in which the asset value and asset type are kept hidden, thereby allowing for multi-asset transactions in which external observers cannot deduce what is being transacted but can verify that the transactions are correct. Cloak is a Confidential Assets scheme built using Bulletproofs.
Cloak is focused on one thing: proving that some number of values with different asset types is correctly transferred from inputs to outputs. Cloak ensures that values are balanced per asset type (so that one type is not transmuted to any other), that quantities do not overflow the group order (in other words, negative quantities are forbidden) and that both quantities and asset types are kept secret. Cloak does not specify how the transfers are authenticated or what kind of ledger represents those transfers: these are left to be defined in a protocol built around Cloak.
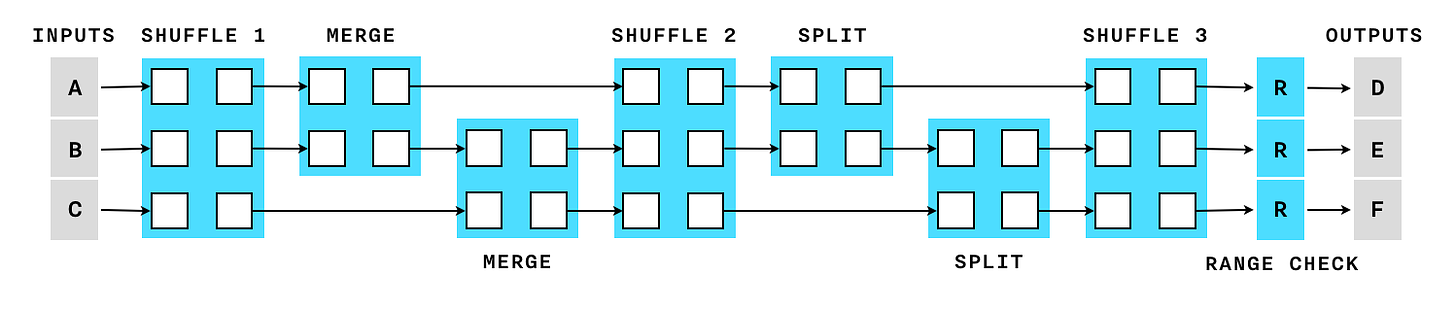
Cloak builds a constraint system using a collection of gadgets like “shuffle”, “merge”, “split” and “range proof” all combined together under a single gadget called a “cloaked transaction”. The layout of all the gadgets is determined only by the number of inputs and outputs and not affected by actual values of the assets. This way, all transactions of the same size are indistinguishable. For example, this is what a 3 input 3 output cloak transaction looks like:
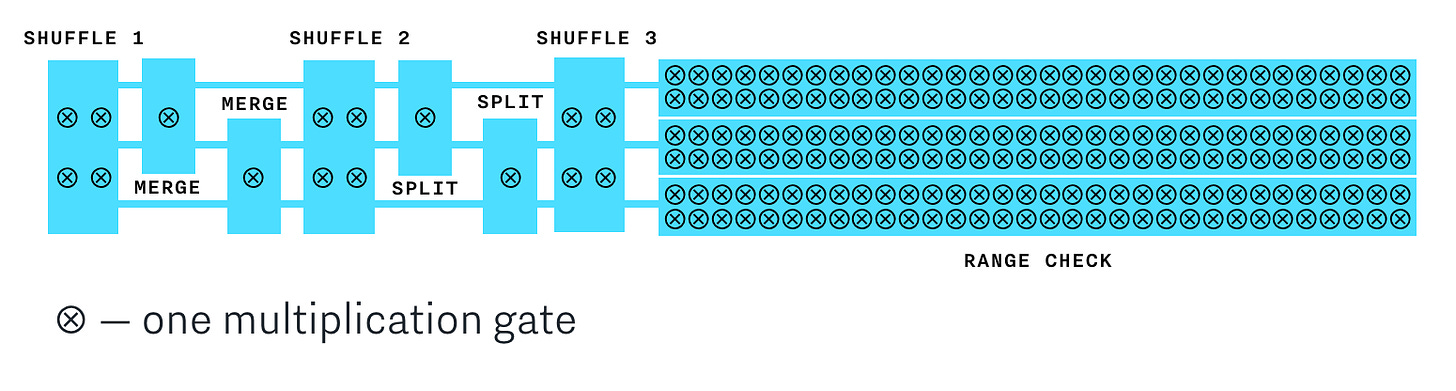
Bulletproofs constraint system turns out surprisingly efficient: compared to a single-asset transaction (such as the Confidential Transactions proposal for Bitcoin) where only range proofs are necessary, the additional constraints and gadgets needed to support the issued assets add less than 20% of the multipliers. And thanks to the inner product proof, the impact on the proof size is close to zero. This is an illustration of the number of multipliers required by each gadget in the Cloak protocol:
To learn more about Cloak, check out its specification. To see the implementation, check out the open-source Cloak GitHub repo.
ZkVM
The goal of ZkVM is to make a smart contract language that allows for confidentiality. It builds upon previous smart contract language work, aiming for an expressive language that runs in a safe environment and outputs a deterministic log. It uses Cloak to validate that encrypted asset flows are correct, and uses Bulletproofs constraint system proofs to add constraints that values are being operated on and contracts are being executed correctly.
ZkVM is still being developed, and you can follow along with progress in the open-source ZkVM GitHub repo.
Review of ‘Proceeding with caution’ a BIS survey on central bank digital currency
Paper by Christian Barontini and Henry Holden, Jan. 8, 2019
Review by Robleh Ali, MIT Media Lab, Digital Currency Initiative
The Bank for International Settlements (BIS) recently released a survey on central bank digital currency (CBDC). This review is in two sections, the first discusses the BIS survey and the second analyses the issues facing central banks as their work on CBDC progresses.
Overall the BIS survey is a very useful insight into central banks’ thinking about CBDC. This usefulness derives from three factors; comprehensive coverage, quantifiable results and segmentation between developed economies and emerging markets.
BIS Survey
Defining CBDC
The paper starts by addressing how to define CBDC. It uses the money flower taxonomy set out in Bech and Garratt (2017) and identifies the four key properties of money as issuer, form, accessibility and technology. A subset of the technology question is the distinction between token based and account-based money.
Token-based and account-based money are differentiated in the paper by how payment verification works. By this definition in a token-based model the recipient does the verification themselves, in an account-based model an intermediary handles verification. This approach draws on a distinction from payment economics and the authors acknowledge that these definitions can vary considerably and can include other descriptions such as value-based money.
These distinctions are driven by underlying technology and there are two problems with applying this taxonomy to digital currencies:
Transaction verification can both be done by recipients who run full nodes and by the mining network.
Digital currencies can use both unspent transaction outputs and accounts as data models for recording transactions.
This makes digital currencies like Bitcoin hard to categorise using the money flower taxonomy because it employs this token/account method to distinguish between different forms of digital money. It may be preferable to draw a distinction between programmable and non-programmable digital money – this taxonomy would delineate more clearly between different types of digital money; bank deposits and e-money on one hand and digital currencies on the other.
In relation to CBDC, this programmable/non-programmable could also be usefully applied to different manifestations of CBDC. For example the Swedish Riksbank is proposing non-programmable CBDC as a complement to cash.
Survey results
One of the strengths of the BIS survey is its coverage – the central banks surveyed account for 80% of the world’s population and 90% of its economy. The survey found that a majority of central banks are working on CBDC, the motivations for doing the work vary and that the work is more focused on understanding this new field of study rather than implementing a CBDC.
Quantifying central banks’ motivation for issuing a CBDC provides some very useful insights into their thinking. The survey draws a distinction between wholesale and general purpose CBDCs and although the applications are different the top motivations are the same – payments safety and payments efficiency.
Differences do emerge when the responses are broken down between emerging markets and developed economies. The biggest difference is financial inclusion, emerging market central banks rate this as the second most important motivation for issuing a widely available CBDC whereas central banks from developed economies rate it last.
The main elements missing from this part of the survey are innovation and competition. It may be that these are included in ‘others’ but it is not specified in the report. While these subjects do not usually fall within the mandate of central banks it is useful for central banks to consider these topics as they certainly affect other surveyed elements (for example payments efficiency is likely to be impaired over the long run from anti competitive behaviour of payment providers).
It is clear from the survey that issuing a CBDC is not imminent. Most of the respondents responded that it was either somewhat or very unlikely that they would issue CBDC in the short to medium term. This supports the assertion at the start of the report that central banks are undertaking conceptual work at present as opposed to working towards an implementation.
The legal authority section of the survey shows that only a relatively small minority of central banks (approximately a quarter) do have or will have legal authority to issue a CBDC. Even for those central banks that do have the strict legal authority, they lack the political authority to issue a CBDC as it would be a fundamental change to how the financial system works. Such a step would therefore need to be led by the government in the shape of the treasury department rather than the central bank whose responsibility in relation to a CBDC would be analysis and implementation . Issuing a CBDC is not like raising or lowering interest rates which an independent central bank can do without reference to any other body, as this is clearly within its mandate – both legally and politically.
The paper concludes that central banks are moving cautiously and collaboratively and will continue to do so. The conclusion highlights spillover risk, that is to say the effect of one jurisdiction issuing a CBDC that becomes widely used in another – effectively forcing the hand of a neighbouring country. This risk cannot be contained solely by central banks collaborating, especially if the impetus to issue a CBDC comes from political momentum either to fundamentally reform the financial system using a CBDC as an instrument or the attraction of the fiscal and strategic benefits from being the first country to issue a widely used CBDC. The following section analyses these issues.
Motivation for issuing CBDC
This section sketches out some of the motivations for a state to issue a CBDC. It covers both some of the rationale considered by central banks to date but also takes account of some broader potential drivers.
The most important fact to recognise when thinking about a digital currency issued directly by a central bank is that – despite the name – the decision to issue a central bank digital currency (CBDC) is not in the gift of the central bank. They are constrained by a mandate given to them by the government and they cannot unilaterally change it in any fundamental way.
For example, monetary policy independence means that the central bank can use the tools at its disposal (for example interest rates) to fulfill its mandate (usually including an inflation target). This does not mean a central bank can change its own mandate, for example by increasing the inflation target or introducing a new factor such as employment. A recent example is the introduction of quantitative easing (QE) after the financial crisis – those central banks that did it needed the consent of the government due to the policy’s quasi-fiscal effects.
Introducing a CBDC would be such a fundamental change to the system that the impetus would likely come from outside the central bank. This section analyses some of the factors that may influence a government when considering whether to issue a CBDC.
Fundamental reform of the financial system
One critique of the post financial crisis reforms is that they were inadequate, wasted the opportunity to reshape the financial system and left a fundamentally flawed system largely undisturbed. Money lies at the heart of the financial system and reforming the way money is created offers the opportunity to change the system in a way earlier reform did not.
Issuing a CBDC could be part of a set of reforms which include implementing full reserve banking and abolishing deposit insurance. This would remove the need for bailouts because the payment system would be separated from the banking system and lending would be fully backed by equity – the costs of a bank’s failures would be borne by its shareholders and not by taxpayers.
It is arguable that public appetite for more radical reforms of the financial system has been underestimated, especially in the light of the political upheaval of various forms which has taken place in several countries the years following the financial crisis. Even the most committed defender of the existing system should recognise that following a future financial crisis another round of technocratic reforms (e.g. marginal changes to capital and liquidity requirements, central clearing of some derivatives and so forth) coupled with more taxpayer funded bailouts is unlikely to assuage public appetite for reform.
Fiscal implications
Fiscal policy falls outside the remit of central banks but it is likely to be a major consideration for countries considering CBDC. The 2016 Bank of England paper on the macroeconomics of CBDC[1] found:
“the establishment of a CBDC regime would also be associated with a permanent increase, ceteris paribus, in ongoing consolidated (government plus central bank) fiscal income flows, due to reductions in net interest expense”
At its core, this is a very simple proposition. Issuing CBDC carries the potential for an immediate fiscal benefit to the issuing government which it can pass on to citizens in the form of lower taxes or increased spending. The cost of doing so could be fundamentally altering the role of banks in the economy (as described above) but this may be seen by many as an added benefit rather than a drawback, especially in the aftermath of another financial crisis with its roots in the banking system.
Strategic implications
The creation of a CBDC also has strategic implications. The BIS survey hinted at the issue by reference to spillovers but these considerations largely fall outside the usual financial and monetary stability frameworks used by central banks. Strategic issues are however highly relevant to other parts of government.
Reserve currency status has a number of benefits beyond lower borrowing costs, for example the ability to effectively impose (or avoid) sanctions by blocking access to international payment systems. Issuing a CBDC carries the potential to alter the balance between reserve currencies and China has shown particular interest in CBDC. This fits with the strategy of China’s Belt and Road Initiative and its effort to increase its soft power.
As CBDC is both a technological innovation as well as an economic tool, the ability to influence how CBDC evolves is potentially very significant. Software is never neutral and carries the values of its creators into the world. Creating a CBDC goes to the heart of questions such as the relationship between citizen, state and corporations and the ability to build surveillance into the core of such a system is one which should be discussed openly and settled democratically. These issues are more important than the economic debate and need to be properly aired.
Technological issues
One of Bitcoin’s attractions is that it introduced an open platform of programmable money. Adding this functionality to national currencies is one of the technological attractions of CBDC. CBDC does not have to be programmable but issuing a non-programmable CBDC risks being a white elephant.
The ability to use smart contracts natively with a national currency opens up the possibility for greater innovation in the financial system of the issuing country. Several governments have indicated their desire to attract and develop financial technology companies and offering CBDC could be a method for doing so. The recent proliferation of ‘stablecoins’ has demonstrated the nascent demand for programmable money denominated in familiar national currencies and if they grow in usage financial stability considerations may require a credit risk-free option to be offered directly by central banks.
Competition issues
Sweden cited the decline of physical cash as a driver for its e-krona project and the decline of cash illuminates a wider issue – competition in payments post-cash. At present, cash is still relatively widely accepted and the infrastructure to support it is still in place but it is arguable that we are in the early stages of its disappearance. This may seem slow at present but – like the bankruptcy of Hemingway's imagination – it will happen gradually then suddenly.
On the current trajectory, card payments are the likeliest replacement for cash over the long term. The question for policymakers is, given the persistent competition problems with card payments, whether they want an increasingly large proportion of the economy in effect paying a transaction tax to private companies. Issuing a CBDC does not necessarily solve these competition problems but it does provide alternative infrastructure for making payments in a national currency which alternative providers could adopt.
Citations
Review of "Proving the correct execution of concurrent services in zero-knowledge”
Paper by Srinath Setty, Sebastian Angel, Trinabh Gupta, and Jonathan Lee, Oct. 2018
Review by Willy R. Vasquez, University of Texas at Austin
Introduction
In “Proving the correct execution of concurrent services in zero-knowledge” by Setty et al. [1], the authors describe a system called Spice that realizes stateful services that are both high performant and verifiable. Stateful services are services that allow clients to manage their data and perform transactions between each other. Some examples include cloud-hosted ledgers which are used to create exchanges or ride-sharing apps, interbank payment networks, and dark pools. Spice is able to achieve 500-1000 transactions per second on a cluster of 16 servers on such types of applications. By using a set-based key/value store with batched verification, they increase transaction throughput by 18,000 - 685,000x over prior work.
The contributions of Spice are:
A definition for the verifiable state machine (VSM) primitive: this primitive captures the requirements of a verifiable stateful service, allowing client privacy from an untrusted verifier. While VSMs were implicitly realized in previous work, the authors provide a concrete definition.
Batched State Verification: the batching of individual state operations for later verification, allowing the cost of individual updates to be amortized.
Concurrent stateful updates: the ability to handle multiple state operations at a single time, allowing for increased throughput in client requests.
SetKV: a concurrent verifiable key/value store that helps realize the Spice VSM. SetKV extends mechanisms for verifying memory and relies on a set-based data structure to construct the verifiable key/value store. SetKV is separate contribution for realizing the Spice VSM and could be used to build a stand-alone untrusted storage service.
The challenges of Spice are:
Batched verification audit: the verification step of SetKV is called an audit, which has a runtime linear in the size of the key/value store. For a large number of entries this can take a noticeable amount of time (e.g. 3.5 minutes for one million entries).
No client privacy from the server: Spice’s threat model is such that the server is trusted to maintain the privacy of client updates, but untrusted to perform correct computations. This threat model is consistent with banks, which maintain account balance privacy but undergo audits to ensure their operations are correct. In Spice, privacy is maintained from other actors in Spice, such as other clients or verifiers.
Summary
Spice is a system that verifies concurrent computations on state without a significant performance cost per operation. Spice generalizes stateful verifiable services into a primitive called a verifiable state machine (VSM) - a state machine with a proof of correctness for each state transition. Compared to previous work which performs per-access state verification, Spice batches the verifications into an audit stage so that costs are amortized over all operations. Because of the way Spice handles state, it can support concurrent stateful operations from multiple clients and guarantee serializability. With batched verification and concurrency, Spice improves throughput performance of state operations significantly over prior work for example applications.
Background
To understand Spice’s contribution, this section provides a background on verifiable computing.
Spice lives in the world of verifiable stateful services, where a client interacts with a service provider to perform some operation on the client’s behalf, and the client would like a guarantee that the operation was performed correctly without leaking the details of the operation. For example, a cryptocurrency exchange acts as a stateful service when it manages the funds of its users. Spice would allow an exchange to provide a proof that a particular operation (e.g. issue, withdraw, transfer) is performed correctly without revealing the details of their customers’ accounts or transactions to an external verifier. Similar examples include ride-sharing apps, mobile payment services like WeChat or Square, and points tracking systems.
A subset of the techniques Spice uses come from a research area called verifiable outsourced computation [4]: a client asks a server to run some computation on a particular input, and the server responds with an answer to the request along with a proof that it performed the computation correctly. The purpose of this proof is to guarantee integrity of computation against a potentially malicious server without requiring the client to recompute everything. It is the equivalent of “showing your work” in elementary school math classes. These days there are three main techniques to verify computation integrity: (1) rely on trusted hardware [2], (2) recompute on multiple servers and take the majority solution [3], (3) or use (non)interactive argument protocols (such as zk-SNARKs). While there are pros and cons to each of the three approaches, advances in systems and crypto techniques has brought much attention to (non)interactive argument protocols, along with their applicability to blockchains [10] and cryptocurrencies [11].
In order to take advantage of (non)interactive argument protocols, programs have to be encoded in a way that allows a server to show that it performed the computation correctly. The traditional encoding thus far has been arithmetic circuits (circuits consisting of fan-in 2 addition or multiplication gates) which can then be used to construct quadratic arithmetic programs (QAPs) or layered circuits for use in argument protocols. Spice treats both argument protocols and program encoding as black boxes, so this review will not go into their details. For an introduction to both, see [4] which reviews the state of the art in 2015.
Spice builds atop stateful verifiable computing systems [5]. State in this context means that there is data that persists across computations, such as anything that relies on database management. Since state persists and may be used as an input to the computation, the client needs a guarantee that all computations are performed on the correct state. The authors abstract stateful verifiable computing into a verifiable state machine (VSM), and show that previous stateful verifiable computing systems implicitly realize this primitive.
Spice
This section describes Spice’s various components and how the overall system is realized.
Verifiable State Machine Primitive
A verifiable state machine (VSM) is a state machine with the ability to verify state transitions without re-execution and without access to the plaintext of all requests, responses, and internal state. Figure 1 shows the dynamics between the the three components of a VSM: a server (concurrent prover) that executes programs and maintains state (backing store), clients that send requests and receive responses that update the state, and verifiers that ensure the integrity of the computation by inspecting a trace (requests, responses, internal state).
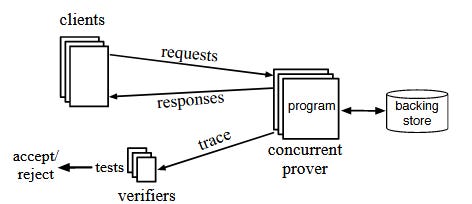
Figure 1. Overview of verifiable state machines [1]
An efficient VSM has the following properties:
Correctness: if a prover is honest, the verifier will always accept;
Soundness: if a prover lies, the verifier will (almost) always catch the prover;
Zero-knowledge: the verifier does not learn anything about the requests, responses, or internal state of the prover;
Succinctness: the trace a verifier receives is small;
Throughput: the prover must be able to handle hundreds of requests per second.
Given this definition, the authors realize this primitive in a system called Spice. They construct Spice from well known and new primitives and prove it satisfies the definition of a VSM.
Spice API for VSMs
In Spice, the programs that a concurrent prover executes are written in C and compiled down to arithmetic circuits for proving with a zk-SNARK system. Spice provides an API for programs to perform state operations on a key/value store such as get(key) and put(key,value) among others. The compiler handles these API operations by what are called exogenous operations: computations that exist outside of the proving infrastructure. As an example, suppose that we wanted a circuit that divides the number a by b. This circuit could be realized as a large collection of additions and multiplications that perform a division (recall arithmetic circuit gates are all additions and multiplications), but that would be inefficient. Instead, the server outsources a/b to a divider outside the proving framework, and verifies that the values it gets, q and r, satisfy the division criteria: a = b*q+r, which only takes two gates. The API Spice provides for the key/value store work in a similar fashion, instead they update a state digest described in the next section.
SetKV
An important innovation in Spice is how it handles state. State is stored in a verified key/value store called SetKV. Previous work relied on using Merkle trees on the state, with the client maintaining the root and subsequent updates providing an updated path and root. Relying on Merkle trees means that each state operation requires a logarithmic amount of hashing operations inside an arithmetic circuit. SetKV, on the other hand, batches verification of state updates by relying on a set-based method for state verification [6]. In SetKV, each individual operation is constant, but the batched verification is linear in the state, which leads to an amortized cost per operation. How SetKV works is that when a state operation occurs, the server keeps track of all reads and writes in their own respective sets, and at a later stage performs an audit to ensure that the read set is a subset of the write set and that there exists a set of key/value pairs which is the difference of the two. The read set and the write set are considered the state digest. The audit function is described in a section below.
Since SetKV has to maintain all reads and writes in their own sets, doing so naively would cause each set to be the size of the state itself. To maintain succinctness, SetKV uses a set collision resistant hash function which is a function that hashes a set of elements into a single element. Since sets do not have any particular order, the hash function is commutative. Since each read or write updates the digest that is maintained, SetKV also needs a hash function that is easily updatable. More specifically, to handle multiple clients, SetKV uses a multi-set collision resistant hash function, which allows for multiple entries of the same element to be in the set. This is realized using MuHash [13, 14], a hash function designed with minimal circuit complexity in mind, allowing for improved performance over standard NIST hash function such as SHA256 or SHA3.
Achieving Zero-Knowledge
Along with succinctness, Spice has to maintain the zero-knowledge property of a VSM. We already discussed how it uses zk-SNARKs to perform computations on private data, but the prover also provides Pedersen commitments [18] to all requests and responses to the verifier and along with the proof of correct computation, proves that it knows the opening to the commitment. The multi-set collision resistant hash function hides the individual elements of the state from the verifier.
Handling Concurrent Requests
For providing concurrency of client requests, Spice uses Lamport clocks to ensure that all requests have some total ordering, as well as a locking mechanism with each key/value pair to prevent conflicts from multiple writers or potentially returning stale data.
Spice Audit
To perform the actual batch verification, the verifier sends an audit request to a prover, which will then prove to the verifier in zero-knowledge that all updates were performed correctly. This requires going through the entire key/value store and ensuring two properties:
Each key is unique
The intersection of the read set with the current state is equal to the write set.
The audit algorithm gets all the keys in the state in a sorted order and checks that they are unique by ensuring they are strictly monotonically increasing and then performs step 2. The verifier would not need to download the entire state since it could perform the above in a streaming manner. Instead of streaming though, the prover performs the audit on behalf of the verifier and provides a proof that it performed the verification correctly. Since the computation can be parallelized, the authors describe a MapReduce computation that can perform the audit. Check out section A.2 in [1] to see how that is structured.
Spice Performance
Spice is built atop a system called Pequin [9] which provides a complete tool-chain for verifiable computation: a C-to-arithmetic circuit compiler as well as a tie-in to libsnark. They add about 2,000 lines of code to support the Spice APIs, and build three applications to evaluate Spice’s performance:
Cloud-hosted ledger service: similar to WeChat or Square, a third party maintains some balance for users where they can issue funds, retire funds, or transfer funds between users. This is compared on Geppetto [15] and Pantry[5].
Payment networks: Bank-to-bank transactions, such as Solidus [16] or zkLedger [17]. In this work they compare against Solidus, though they note a different threat model. They evaluate crediting, debiting, and transferring funds.
Dark pool: An opaque securities exchanges with submit and withdraw operations. This is compared on Geppetto [15] and Pantry [5]. Since submit and withdraw are similar only submit is evaluated.
Something to keep in mind when comparing Spice against Pantry and Geppetto is that given a state S: Pantry takes O(log(|S|)) number of operations for any state update; Geppetto takes O(|S|) number of operations for any state update; Spice takes O(1) number of operations for any state update, but takes O(|S|) in the audit. So the question the authors ask is at what state size |S| does Spice outperform Pantry and Geppetto in terms of circuit complexity, throughput, and latency for the example applications?
Circuit Complexity: the number of constraints depends on the size of the state. For one million key/value pairs in the state, Spice uses 57x fewer constraints than Pantry and 2,000x fewer constraints than Geppetto. Even with the audit, Spice can still get lower per-operation circuit cost at a sufficiently spaced out number of state operations. For example, after around 7,000 state operations Spice requires less constraints than Pantry and Geppetto.
Throughput: they measure the number of storage operations performed by the prover per second as the number of cores increases. They load the state with one million entries and compare against uniform queries versus Zipfian queries. Spice has a linear speedup increasing the number of cores. At a single core Spice’s throughput is 92x higher than Pantry and 1,800x faster than Geppetto. At 512 cores Spice’s throughput is 35,100x higher than Pantry and 685,000x higher than Geppetto.
Latency: the time to produce the audit dictates the latency of the state verification. Running the MapReduce audit computation on a state of one million entries takes 3.63 minutes (3 minutes, 38 seconds), so if it is run every k minutes the latency would be k+3.63 minutes.
Verification of each proof takes around 3ms, so for audit alone a verifier would take 3.2 CPU-seconds to verify the audit.

For the applications, Spice shows a linear increase in performance with the number of CPUs, and is able to satisfy the VSM throughput requirement. The figure above shows throughput for number of cores for each function.
Contributions & Challenges
Spice introduces a variety of different techniques, of which we discuss the contributions and challenges here.
Contributions
Batched State Verification
A large contribution is the idea of batched state verification realized in SetKV for amortized costs for improved performance. The authors describe example applications where such batching can be tolerated: (a) systems that can survive a failed verification (e.g. through rollbacks); and (b) systems that have external mechanisms to punish failed verification (e.g. fines or other costs).
Concurrent support for state
Along with batched verification, Spice is also the first stateful verifiable computing system to allow for concurrent state operations. Because ordering does not matter in the multi-set collision-resistant hash function, as long as dependent requests are handled correctly through locks, then state aggregation can occur in any order.
SetKV
SetKV is a verified key/value store that builds atop Concerto [6]. The SetKV construction could be applicable to other systems relying on verified key/value store. The original Concerto paper described running the audit and get/put operations on trusted hardware, but this SetKV provides algorithmic improvements over Concerto and shows trusted hardware can be replaced with efficient argument protocols for integrity of computation.
Challenges
Batched State Verification
A challenge of batched state verification is that a rollback of computations performed for some epoch would constitute lost progress and necessitate re-execution of all computations for that epoch. The issue here is that the use of the multi-set collision-resistant hash function to encode the read/write sets means that a verifier cannot identify which is the failing request/response pair in the batched verification.
Another challenge that comes from batched verification is the linear time requirement to audit the state. Every time a verifier asks for an audit, the prover has to scan the entire state and prove that it performed the audit correctly. Though by setting a sufficiently large time-step at which audits occur, the amortized cost is lower than the per-operation cost of previous work.
No client privacy from Server
While the client gets a guarantee that the server performed the computation correctly, the server sees the plaintext of all requests and responses. Though, the client is guaranteed privacy from the verifiers knowing the contents of both requests and responses. In order to use Spice, one has to consider use cases where a third party is trusted for privacy but not for integrity. The use of financial applications seems to be one such case, where you may be okay revealing amounts (because secrecy is provided through law or other mechanisms) but financial entities may try to cheat. More work is required on adding privacy guarantees.
Blockchain Connection
Spice is connected to the blockchain world by the techniques that are used to construct it, as well as the types of services that it can provide.
As described, Spice relies on argument protocols instantiated with zk-SNARKs. There is much work going on at the intersection of zk-SNARKs and blockchains, and Spice demonstrates a new point in this solution space. While not explicitly using a blockchain in its back-end, one could be used to provide similar decentralization guarantees as Sequence [19] or Amazon QLDB [20]. Like most other work involving zk-SNARKs in this space, this is an experiment on the use of new technologies. While zk-SNARKs are more well known, other techniques like the multi-set collision resistant hash function are not yet as battle-tested. However, the authors show significant performance improvements with the latter.
The authors note that a VSM can implement any request-processing application that interacts with a database, including smart contracts and cloud-hosted ledgers. Spice achieves similar similar guarantees implicitly via the VSM as the smart contracts described in Hawk [8]. Many existing services that realize cloud-hosted ledgers rely on trusted hardware for verifiability guarantees. Both Hyperledger Fabric [12] and Chain’s Sequence [19] use blockchains inside enclaves to maintain verifiability. Using Spice, the clients will put their trust in cryptographic guarantees/primitives rather than hardware. The issue of privacy would still need to be addressed though.
Conclusion and Future Work
Overall, Spice provides a new way to offer verifiable stateful services by using batched verification, and brings verifiable computing closer to the mainstream.
Some future work mentioned in the paper:
Applying DIZK [7] to further parallelize and scale out Spice’s audit;
Hiding the sender identity in payment networks and other general client privacy guarantees;
Apply argument protocols without a trusted setup such as Bulletproofs;
Leverage metadata inside a value to implement other mutual-exclusion primitives and other isolation levels.
Citations
[1] Srinath Setty, Sebastian Angel, Trinabh Gupta, and Jonathan Lee, “Proving the correct execution of concurrent services in zero-knowledge,” https://www.usenix.org/system/files/osdi18-setty.pdf. Full version: https://eprint.iacr.org/2018/907.pdf
[2] COSTAN,V., AND DEVADAS, S. Intel SGX explained. Tech.rep., Cryptology ePrint Archive, Report 2016/086, 2016.
[3] J. Teutsch and C. Reitwießner, “A scalable verification solution for blockchains,” 2017, https://people.cs.uchicago.edu/∼teutsch/papers/truebit.pdf.
[4] M. Walfish and A. J. Blumberg. Verifying computations without reexecuting them: From theoretical possibility to near practicality.Communications of the ACM, 58(2), Jan. 2015.
[5] B. Braun, A. J. Feldman, Z. Ren, S. Setty, A. J. Blumberg, and M. Walfish. Verifying computations with state. In Proceedings of the ACM Symposium on Operating Systems Principles (SOSP), 2013.
[6] A. Arasu, K. Eguro, R. Kaushik, D. Kossmann, P. Meng, V. Pandey, and R. Ramamurthy. Concerto: A high concurrency key-value store with integrity. In Proceedings of the ACM International Conference on Management of Data (SIGMOD), 2017.
[7] H. Wu, W. Zheng, A. Chiesa, R. A. Popa, and I. Stoica. DIZK: A distributed zero-knowledge proof system. In Proceedings of the USENIX Security Symposium, 2018.
[8] A. Kosba, A. Miller, E. Shi, Z. Wen, and C. Papamanthou.Hawk: The blockchain model of cryptography and privacy-preserving smart contracts. InProceedings of the IEEE Symposium on Security and Privacy (S&P), 2016.
[9] Pequin: An end-to-end toolchain for verifiable computation, SNARKs, and probabilistic proofs. https://github.com/pepper-project/pequin, 2016.
[10] I. Meckler and E. Shapiro. Coda: Decentralized cryptocurrency at scale. https://codaprotocol.com/static/coda-whitepaper-05-10-2018-0.pdf, 2019.
[11] E. Ben-Sasson, A. Chiesa, C. Garman, M. Green, I. Miers, E. Tromer, and M. Virza. Zerocash: Decentralized anonymous payments from Bitcoin. In IEEE Symposium on Security and Privacy, 2014.
[12] Hyperledger. Hyperledger Fabric. https://www.hyperledger.org/projects/fabric, 2019.
[13] M. Albrecht, L. Grassi, C. Rechberger, A. Roy, andT. Tiessen. MiMC: Efficient encryption and cryptographic hashing with minimal multiplicative complexity. InProceedings of the International Conference on the Theory and Application of Cryptology and Information Security (ASIACRYPT), 2016.
[14] M. Bellare and D. Micciancio. A new paradigm for collision-free hashing: Incrementality at reduced cost. InProceedings of the International Conference on the Theory and Applications of Cryptographic Techniques(EUROCRYPT), 1997.
[15] C. Costello, C. Fournet, J. Howell, M. Kohlweiss,B. Kreuter, M. Naehrig, B. Parno, and S. Zahur. Geppetto:Versatile verifiable computation. In Proceedings of the IEEE Symposium on Security and Privacy (S&P), May 2015.
[16] E. Cecchetti, F. Zhang, Y. Ji, A. Kosba, A. Juels, and E. Shi. Solidus: Confidential distributed ledger transactions via PVORM. InProceedings of the ACM Conference on Computer and Communications Security(CCS), 2017.
[17] N. Narula, W. Vasquez, and M. Virza. zkLedger:Privacy-preserving auditing for distributed ledgers. In Proceedings of the USENIX Symposium on Networked Systems Design and Implementation (NSDI), 2018.
[18] T. P. Pedersen. Non-interactive and information-theoretic secure verifiable secret sharing.In Advances in Cryptology – CRYPTO’91, volume 576 of LNCS, pages 129–140. Springer, 1992.
[19] Chain. Introducing Sequence. https://blog.chain.com/introducing-sequence-e14ff70b730, 2019.
[20] Amazon. Amazon Quantum Ledger Database. https://aws.amazon.com/qldb/, 2019.
Previous Issues
Other Great Curation
Lots of companies have started (Bitmex-style) research arms recently. e.g. Circle Research and Token Daily Research.
Upcoming Conferences
There’s a new ACM conference, Advances in Financial Technologies. Oct 21-23, Zurich, Switzerland. Submissions due May 24.
Scaling Bitcoin, September 11th-12th, Tel Aviv. Submissions due June 10.
Great list of academic cryptocurrency conferences from BSafe.network
Community Notes
Join our Telegram channel here for discussion on Cryptocurrency Research!
If you have any feedback, please just respond to this email directly. We’d love to hear from you. Thanks!
Disclaimer: All content is for informational purposes only and not intended as investment advice.
Subscribe to Cryptoeconomic Systems Journal & Conference Series
This journal and conference series aims to be a premier venue for cross-disciplinary research and meta-analyses around the topics of cryptocurrency and blockchain technology.


